Lecture 3: Combinatorial and Axioms of Probability Practice Excercises

Lecture Notes 11 Minutes

Authors:

  1. Irtaza Haider  [msds18021@itu.edu.pk]
  2. Gulraiz Ali  [msds19021@itu.edu.pk]
  3. Hafiz Muhammad Sheharyar  [msds19065@itu.edu.pk]

Agenda:

  • Cover exercises related to homework#1
  • Topics Discussed
    • Basic Principle of Counting
    • Permutation
    • Combination
    • Multinomials
    • Conditional Probability
    • Law of Total Probability

Before starting the lecture, the discussion of assignment was started with a few jokes about those who emailed to Sir remarking that the course is too basic, yet more than half of people were having difficulty in solving the questions of homework. Only a few were comfortable with the homework.

In case of any problems TA’s can be contacted: 

  1. Naufil (naufil.hassan@itu.edu.pk) available on lecture days
  2. Aimal (rehman.aimal@gmail.com) available 40 hours per week

Pro Tip: The person who is found gossiping during lectures will become Sir’s favorite student and that favorite will have to sit near sir on stairs for the whole semester. So, avoid discussions with fellows during lecture.

According to HEC rules this course will primarily cover the following topics:

  1. Discrete Probability
  2. Continuous Probability
  3. Statistics
  4. Linear Algebra

So, we will be covering this course robustly.

Students Question: Can you please provide the solution manual of the book?

Answer: Internet is a good resource for it but if you don’t understand just go to the TAs.

Student’s Question: Can you please explain us about lecture notes?

Answer: Lecture notes must be submitted in two days after class within 48 hours. For example, if we have lecture on Monday the lecture notes must be uploaded on Wednesday before 05:30 pm. Moreover, the TAs will give access to the blog where lecture notes are to be posted. Try to record the interactions in lecture notes. Links, pictures and good examples can also be added. Format of the notes is text which can be written simply but equations must be written in Latex format.

Our today’s lecture is merely a revision of previous homework and exercises.

Basic Principle of Counting

The Fundamental Counting Principle (also called the counting rule) is a way to figure out the number of outcomes in a probability problem.

Image result for counting principle

Definition:

Suppose that two experiments are to be performed. Then if experiment 1 can result in any one of m possible outcomes and if, for each outcome of experiment 1, there are n possible outcomes of experiment 2, then together there are mn possible outcomes of the two experiments.

Examples:

Question #1

A small community consists of 10 women, each of whom has 3 children. If one woman and one of her children are to be chosen as mother and child of the year, how many different choices are possible?

Correct Solution

By regarding the choice of the woman as the outcome of the first experiment and the subsequent choice of one of her children as the outcome of the second experiment, we see from the basic principle that there are 10 * 3 = 30 possible choices.

Permutation

Definitions:

  • Number of ways things can be ordered
  • A permutation is an arrangement of all or part of a set of objects, with regard to the order of the arrangement.
Image result for Permutation

Equation:

The number of permutations of n objects taken k at a time is determined by the following formula:

P(n,k)=nP_k=\frac{n!}{(n-k)!}

Examples:

Question #2

Ms. Jones has 10 books that she is going to put on her bookshelf. Of these, 4 are mathematics books, 3 are chemistry books, 2 are history books, and 1 is a language book. Ms. Jones wants to arrange her books so that all the books dealing with the same subject are together on the shelf. How many different arrangements are possible?

Incorrect Solution:

10!

Not correct since all the possible arrangements of books are not valid in our problem we have the constraint of keeping the books of same subjects together!!

So we need to think how to count only the possibilities in which books can be arranged while making sure that the books of same subject be placed together.

Correct Solution

(4! *  3!  *  2! * 1!  ) * 4!

Do you think its the right answer??

Well yes it is the right answer. Let me tell you how, first let us calculate in how many ways the Mathematics books can be arranged while keeping all of them together, as there are 4 Mathematics books we can arrange the Mathematics books in 4! ways. Similarly Chemistry books can be arranged in 3! ways, History books in 2! and finally Language books in 1!.

So the total number of possibilities we have so far incorporated can be found by using the basic principal of counting, and that gives us, (4! *  3! * 2! * 1!)

But wait !! what about the last 4! in the solution ?? Where does that come from ??

Yes, you are right we forgot to consider that the groups of books can also be arranged in different patterns, and as we have 4 groups these can be arranged in 4! different arrangements.

Student’s Question: Why are we putting multiplication instead of addition ?

Answer: Multiplication is being used because for every course all other course’s order is valid. E.g. For Mathematics all possible orders of Chemistry are valid. It means that for every arrangement of Mathematics books every arrangement of Chemistry books is valid.

Student’s Question: Why isn’t it 10! ?

Answer: Because all possible combinations are not allowed. e.g. It is not allowed to have 1 Mathematics then 1 Chemistry then 1 History … All Mathematics books should be together, and all other books of same subjects should be together. If we had 10 different books with no restriction of being together then it will be 10!.

Question #3

How many different letter arrangements can be formed from the letters PEPPER?

Incorrect Solution:

6!

Not correct, since it considers the P’s and E’s to be different,which are actually not different. For example if we name the P’s to be P_1,P_2,P_3 it considers P_1 E P_2 P_3 E R and P_2 E P_1 P_3 E R as different arrangements which is wrong both are just PEPPER.

Correct Solution:

\frac{6!}{3!\ast 2!\ast 1!}

Since the repeating P’s and E’s are all same in a sense that any P substituted with any other P makes no difference, so we need to remove this relative order from the equation. That’s why we are removing this part from the equation by diving with 3!*2!*1!

Student’s Question: Why we are dividing by 3! and 2! ?

Answer:  As the order of P’s does not matter, we are dividing by number of possible ways 3 P’s can be arranged which is 3! And same is the case with 2 E’s whose possible combinations are 2!

Combination

In mathematics, a combination is a selection of items from a collection, such that (unlike permutations) the order of selection does not matter.

Definitions:

  • Group of r items could be selected from n items
  • A combination is a selection of all or part of a set of objects, without regard to the order in which objects are selected.

Equation:

C(n,k)=\binom{n}{k}=\frac{n!}{k!(n-k)!}

Examples:

Question #4

From a group of 5 women and 7 men, how many different committees consisting of 2 women and 3 men can be formed? What if 2 of the men are feuding and refuse to serve on the committee together?

Correct Solution

a) \binom{5}{2}\binom{7}{3}

b) \binom{5}{2}\binom{5}{3}\dotplus\binom{5}{2} \binom{2}{1}\binom{5}{2}

b) \binom{5}{2}[\binom{7}{3}-\binom{5}{2}] (Alternative Solution)

For Part(a), it is pretty straight forward we have to choose 2 women from the group of 5 women and 3 men from the group of 7 men so we simply multiply the number of out comes we have for choosing women and men.

For Part(b), we divide the solution in 2 parts: In first part, we calculate the number of outcomes in which none of the two feuding men are picked. And in second part, we calculate the number of outcomes in which one of the feuding men is picked. And finally we add the number of outcomes from both parts.

Incorrect Solution of Part (b)

(1)   \binom{5}{2}\binom{5}{2}\binom{2}{1}

Not correct since it forces a selection from the feuding men.

(2)   2\binom{5}{2}\binom{6}{3}

Not correct since it also forces selection of one of the feuding men.

(3)   \binom{5}{2}\binom{6}{3}\dotplus\binom{5}{2}\binom{6}{3}

Not correct since it, although excludes one of the feuding men but, forces selection of the remaining feuding man.

Question #5

Consider a set of n antennas of which m are defective and n − m are functional and assume that all of the defectives and all of the functional are considered indistinguishable. How many linear orderings are there in which no two defectives are consecutive?

Incorrect Solution

m! ways to arrange defective pieces

(n-m)! ways to arrange functional pieces

m!(n-m)! \binom{ n-m+1 }{m}

Because, we cannot distinguish between functional antennas themselves and defective antennas themselves so the correct solution will not contain the combinations of   m!(n-m)! .

Correct Solution

\binom{ n-m+1 }{m}

Book Explanation: Imagine that the n - m functional antennas are lined up among themselves. Now, if no two defectives are to be consecutive, then the spaces between the functional antennas must each contain at most one defective antenna. That is, in the n - m + 1 possible positions—represented in Figure 1.1 by carets—between the n - m functional antennas, we must select m of these in which to put the defective antennas. Hence, there are \binom{ n - m+1 }{m} possible orderings in which there is at least one functional antenna between any two defective ones.

Can you answer this simple question ???

Image result for Permutation

Multinomial

Equation:

\binom{n}{n_1,n_2,...n_r}= \frac{n!}{n_1!n_2!...n_r!}

Question #6

A police department in a small city consists of 10 officers. If the department policy is to have 5 of the officers patrolling the streets, 2 of the officers working full time at the station, and 3 of the officers on reserve at the station, how many different divisions of the 10 officers into the 3 groups are possible?

Correct Solution

\binom{10}{5}\binom{5}{2}\binom{3}{3}

=\frac{10!}{5!(10-5)!}\ast\frac{5!}{2!(5-2)!}\ast\frac{3!}{3!(3-3)!}

=\frac{10!}{5!5!}\ast\frac{5!}{2!3!}\ast\frac{3!}{3!0!}

=\frac{10!}{5!3!2!}

We can also verify this from the formula of multinomial presented above.

\binom{10}{5,3,2}= \frac{10!}{5!3!2!}

Above sequence represents the ways Street police, Station Police and Reserve Police can be arranged respectively.

Question #7

In order to play a game of basketball, 10 children at a playground divide themselves into two teams of 5 each. How many different divisions are possible?

Correct Solution

\frac{\binom{10}{5}}{2}

Incorrect Solution: \binom{10}{5}

Correct Solution:    \frac{\binom{10}{5}}{2} = 126

Explanation:  If we have \binom{10}{5} , then it means we are having both ordering of same teams

Team_1 Team_2 .

Team_2 Team_1 .

Which are consisting of exactly same players, so we divide it with 2 to choose half of them. Hence the answer is \frac{\binom{10}{5}}{2} .

Question #8

A student has to sell 2 books from a collection of 6 math, 7 science, and 4 economics books. How many choices are possible if (a) both books are to be on the same subject? (b) the books are to be on different subjects?

Correct Solution

(a)   \binom{6}{2} + \binom{7}{2} + \binom{4}{2}

(b)   \binom{6}{1} \binom{7}{1} + \binom{6}{1} \binom{4}{1} + \binom{7}{1} \binom{4}{1} = 6*7+6*4+7*4 =94

For Part(a), we are separately computing the Combinations of each subject so that only the same subject books are picked together. For Part(b), the multiplication between combinations make sure 2 books are of separate subjects and the addition is ensuring that all possible couplings (e.g. Math with Science or Math with Economics) are handled.

Question #9

Consider the following technique for shuffling a deck of n cards: For any initial ordering of the cards, go through the deck one card at a time and at each card, flip a fair coin. If the coin comes up heads, then leave the card where it is; if the coin comes up tails, then move that card to the end of the deck. After the coin has been flipped n times, say that one round has been completed. For instance, if n = 4 and the initial ordering is 1, 2, 3, 4, then if the successive flips result in the outcome h, t, t, h, then the ordering at the end of the round is 1, 4, 2, 3. Assuming that all possible outcomes of the sequence of n coin flips are equally likely, what is the probability that the ordering after one round is the same as the initial ordering?

Correct Solution

Total Possibilities = 2^{n}

Valid ways = n+1=\sum_{k=0}^{n}1 , where k=number of heads

Probability of same ordering after one round = \frac{n+1}{2^{n}}

The solution goes with the condition that for the ordering to remain the same, no head should be encountered once a tail has appeared.

Conditional Probability

Definition:

  • The probability of an event  A, given that another B has already occurred.
  • Conditional probability is defined as the likelihood of an event or outcome occurring, based on the occurrence of a previous event or outcome

Equation:

P(A|B)=\frac{P(A\cap B)}{P(B)}

Where:

  • P(A|B) – the conditional probability; the probability of event A occurring given that event B has already occurred
  • P(A ∩ B) – the joint probability of events A and B; the probability that both events A and B occur at the same time
  • P(B) – the probability of event B

Question #10

A group of 6 men and 6 women is randomly divided into 2 groups of size 6 each. What is the probability that both groups will have the same number of men?

Correct Solution:   

\frac{\binom{6}{3}\binom{6}{3}\frac{1}{2} }{\binom{12}{6}\frac{1}{2} }

The Numerator holds the 2 grouping Combinations and the Denominator holds all targeted possible arrangements within the sample space. We divided both the sides of fraction by 1/2 since the groups are indistinguishable. 

NOTE: In exams, write a note at the top of the question the assumption you are proceeding with, i.e. distinguishable or indistinguishable

Question #11

A total of n balls are sequentially and randomly chosen, without replacement, from an urn containing r red and b blue balls (n ≤ r + b). Given that k of the n balls are blue, what is the conditional probability that the first ball chosen is blue?

Law of Total Probability

Definition:

If B1,B2,B3,⋯ is a partition of the sample space S, then for any event A we have.

P(A)=\sum_{i}P(A\cap B_i)=\sum_{i}P(A|B_i)P(B_i)

What is ‘Partition’?

–  Subsets of S

–  A1 ∪ A2 … An = S

–  Ai  ≠ Φ

–  Ai  ∩ Aj = Φ

Intuition

If your sample space is divided into divisions, Law of Total Probability says that to calculate the Probability of an event A within that sample space you need to add the parts of P(A) that falls into each partition

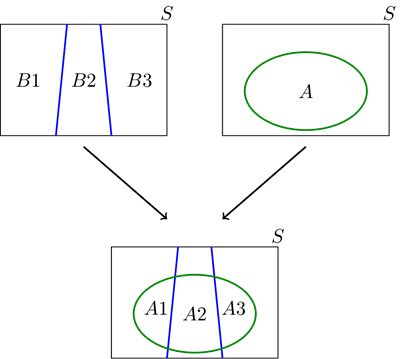
Example:

In a certain country there are three provinces, call them B1, B2, and B3 (i.e., the country is partitioned into three disjoint sets B1, B2, and B3). We are interested in the total forest area in the country. Suppose that we know that the forest area in B1, B2, and B3 are 100km2, 50km2, and 150km2, respectively. What is the total forest area in the country? If your answer is

100km2+50km2+150km2=300km2

you are right. That is, you can simply add forest areas in each province (partition) to obtain the forest area in the whole country. This is the idea behind the law of total probability, in which the area of forest is replaced by probability of an event A.

Concluding Remarks

At the end of the class it was announced that the class will continue with with the “A total of n balls…” problem as we ran into the digression of Law of Total Probability.

Published by hafizmuhammadsheharyar

Published

15 thoughts on “Lecture 3: Combinatorial and Axioms of Probability Practice Excercises”

  1. The door should be unlocked with a permutation, and not a combination! Because order of the characters matter, that’s a classic!
    Great job on the lecture notes, very engaging!

    Liked by 4 people

    Reply

  4. Kindly correct me if I am wrong.
    Solution of Question 10 says, in its explanation to be more specific, that the groups ‘aren’t indistinguishable’ or simply they are distinguishable. Considering what I remember from lecture, we are not supposed to divide by 2! in numerator and denominator if this really is the case.

    Like

    Reply

    1. i think the answer of Q.4 b) will be \binom{5}{2}[\binom{7}{3}-\binom{5}{1}] (Alternative Solution)
      as we are ignoring 2 conflicting persons
      correct me if i am wrong

      Like

      Reply

Leave a comment